1. 概要: Michaelis-Menten 式とは
2. 準備 1: 反応速度定数と最初の式
3. 準備 2: P からの逆反応は起こらない
4. 本番 1: K_M の導入
5. 本番 2: V を [S] の式で表す
6. 本番 3: V_max の導入と K_M の解釈
7. 関連項目
   • 酵素メインページ
   • Lineweaver-Burk plot
   • 酵素の阻害

概要: Michaelis-Menten 式とは

誤解を恐れずに言えば、Michaelis-Menten とは 酵素反応の速度が、基質濃度によってどのように影響されるかを知りたくて式をいじっているうちに、使える定数が得られちゃった ということである。

生化学の教科書では、目的が曖昧なまま式変形が始まるのがわかりにくいと常々思っていたので、歴史的背景として正しいのかどうかわからないが、以下のような問題設定でこのページを作ってみたい。

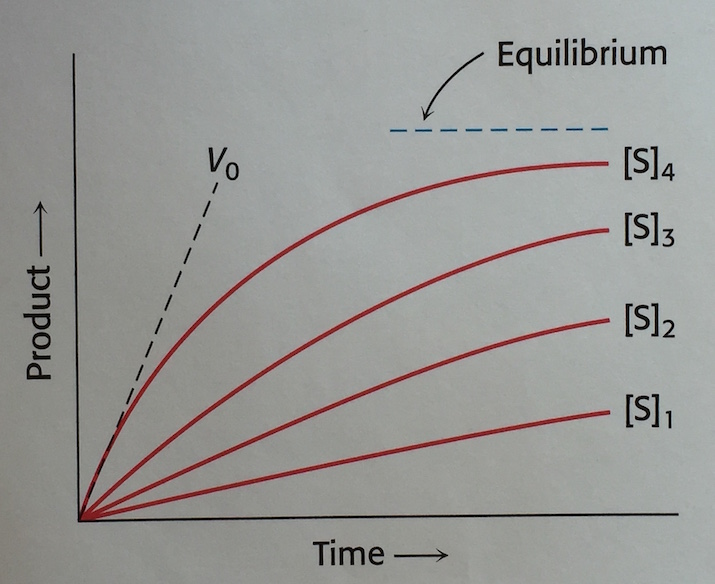
• いろいろと基質濃度 [S] を変えて酵素反応実験をしてみると、図 (ref 3) みたいな結果になる。縦軸は反応生成物量、横軸は時間。
• なんか [S] が高いほど反応速度 V も高い気がするから、両者には関係があるんだろう。
• OK, ひとつ [S] から V を計算するための式でも作ってみるか。
• ただし基質は酵素で消費されて減っていくから、実験データを使いたいときには、t = 0 の時点での基質濃度 [S₀] しか使えないね。
• ってことは、酵素反応の速度 V も t = 0 の時点の V₀ で考えるのが良さそうだ。

このページの説明は、ES の形成過程が迅速平衡であるという仮定に基づいたオリジナルの Michaelis と Menten の方法でなく、のちに Briggs と Haldane が改良した方法で Michaelin-Menten の式 (式 12) を導いている。この方法では、ES の形成過程を定常状態と仮定することで、一般的条件でもこの式が成立するような改良が施されている (6)。いわゆる「迅速平衡法」ではなく「定常状態法」である。

準備 1: 一般的な酵素反応の定式化

図を見てみると、酵素濃度を一定にしたまま基質濃度を上げた場合、反応速度がプラトーに達している。これは 酵素 E と基質 S が複合体 ES を形成する ことを意味してるんだろう。酵素の active site が基質で占められている状態っていうこと。

まずは、ES を介した反応を式で表すところから始めてみよう。一連の説明は Berg の Biochemistry (Amazon link) に基づいている。

: 実際に、基質が結合した状態で、多くの酵素の結晶構造が解かれている。
: NMR などの分光分析でも、基質と酵素の結合は確認されている。

反応式は次のようになる。式 1 としておこう。P は product で、反応生成物を示す。

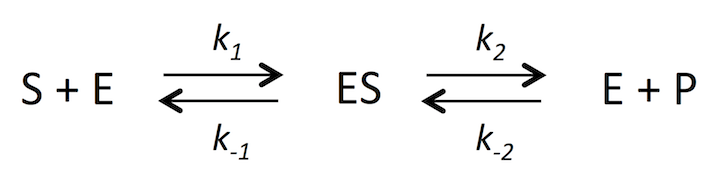    式 1

ここで k₁、k_-1、k₂、k_-2 は 反応速度定数 reaction rate constant である。

反応速度定数とは 基質の濃度と反応速度を結びつける定数 であり、一般に A + B → C という反応では、反応速度とは C の濃度の時間変化率 d[C]/dt であり、反応速度定数 k を用いて以下の式で与えられる。

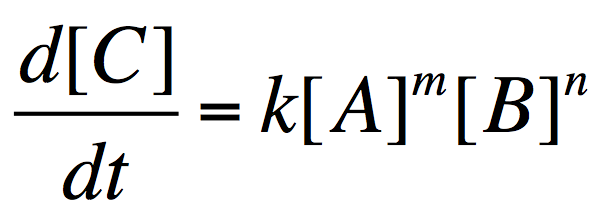
m, n は反応の次数であり、実験によって求められ、化学反応式から推定することは原則としてできないというやっかいな数字である。

式 1 では、たとえば酵素と基質の複合体 ES が合成される速度は d[ES]/dt = k₁ [E]^m [S]ⁿ で与えられることになる。ここでもう一度図を見てみると、t = 0 の付近では P の生成速度が [S] と比例しているので、[ES] が合成される速度も [E] や [S] と比例、つまり m = n = 1 でいいような気がしてくる (本当か？)。実際、Biochemistry では説明なしに m = n = 1 としている。

k が平衡定数 equilibrium constant や解離定数 dissociation constant ではないことに注意しよう。表記が似ているが、Michaelis-Menten を学ぶ上では、まず反応速度定数をしっかり理解することが重要。

準備 2: P からの逆反応は起こらないという仮定をおく

ここでは反応のごく初期、t = 0 近辺を考えているので、最終生成物が分解される E + P → ES の反応は起こらないと仮定してしまおう。k_-2 = 0 ということ。すると、式 1 は次のようになる。

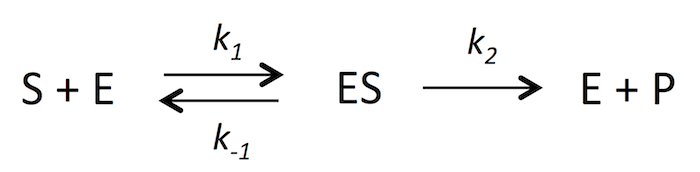    式 2

これで準備完了。いよいよ、本来の目的である反応速度 V₀ と S₀ を繋げる式を作ってみる。

本番 1: 式を立て、ES 量が一定という仮定をおき、定数 K_M を導入

V₀ というのは P が生成する速度のことなので、反応係数の定義から、式 2 の k₂ を使って次のように表すことができる。

ES っていうのは、式 2 でみるように作られたり分解されたりしている。これも反応係数の定義から、

物事を単純化するために、1924 年に Briggs と Haldane という人たちが ES 量は一定である と大胆に仮定してしまった。つまり ES が作られる量 = ES が分解される量ということ。これを受け入れると、式 4 と 5 から

式 6 を変形させると、左辺に濃度、右辺に定数をきれいにまとめることができる。右辺が定数だけになったということは、この式は反応によって一定の値をもつということである。

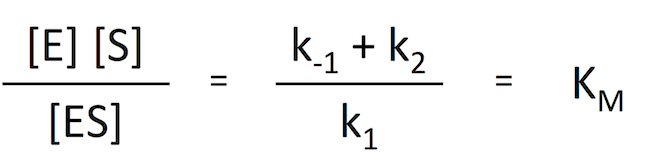    式 7

定数とはいえ、k が 3 つも出てくるとややこしいので、この式をまとめて K_M と置いてしまう。これが Michaelis-Menten 定数 である。

この定数の意味するところは、まだこの時点では明らかでない。さらに式変形を進めていくことで、K_M のもつ意味がわかってくる。

本番2: V を [S] の関数で表すために式変形を続ける

式変形に一生懸命になり、Michaelis-Menten 定数が出てきたことで満足してしまってはいけない。初期の目的を思い出そう。t = 0 付近で V を [S] の関数で表す ことが目的だったはず。

そう考えると、式 3 が意外と目的に近い形になっているが、[ES] が邪魔だったことに気づく。なんといっても [ES] は中間体なので、実験的に値を求めることができない。なんとかして消去したい。

実は、本番 1 の作業は式 3 から [ES] を消去するためのものだったのである。式 7 を変形すると

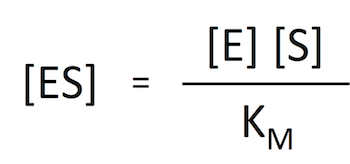    式 8

であるから、これを式 3 に代入すればよいわけである。

単純に代入すると [ES] は首尾よく消去できるが、右辺に [E] と [S] が残ってしまう。これは良くない。V は変数であり、これを変数 [S] の関数として表したいのに、もう一つ変数 [E] が必要になってしまうということだからである。

言い換えれば、y = ax + b のような形の式を作って「x から y が計算できるから、実験で x を求めればいいね」という結論にしたかったのに、y = ax + z + b のように新たな変数 z が含まれてしまっているようなものである。

ちなみに [E] は「酵素濃度」ではなく「基質と結合していない酵素濃度」なので、単純には測定不可能。

そこで、[E] をのちに消去できるような形に一工夫してから、式 8 を式 3 に代入する という手段をとることにする。

では、式変形を始めよう。酵素の全体の濃度を [E]_T とすると、

つまり

となる。これを式 8 に代入したものが式 9、式 9 を [ES] について解いたものが式 10 である。[E] は反応途中の値なので時間とともに変化する変数であるが、[E]_T は実験の初期値であり、定数であることに注意しよう。

式 10 を式 3 に代入すれば、

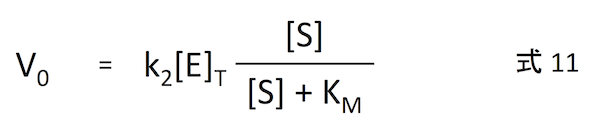
となり、ようやく目的を達成できたわけである。

反応の初期 (t = 0 に近いとき) の反応速度 V₀ は、基質濃度 [S] を用いて式 11 のように表すことができる。k₂、[E]_T はその反応系において定数であり、要は y = ax のように線形の比例関係となる。

なお、ここでは Berg の Biochemistry に習って酵素濃度は [S] で表しているが、V₀ に合わせた表記として [S]₀ とするのが望ましいように思う。実際に [S]₀ と書いている論文もある (5)。

本番3: V_max の導入と K_M の解釈

式 11 で既に目的を達しているわけだが、k₂ や [E]_T をもう少し意味のある定数でクールに表したい。そこで 酵素反応の最大速度 V_max という値を考えてみる。

式 2 が正しいとすると、反応速度が最大になるのは、全ての酵素が基質と結合しているとき である。つまり

このとき、当然 [E] = 0 である。式 2 や反応定数の定義から、

この V_max を式 11 に代入することで、Michaelis-Menten の式 が得られる。

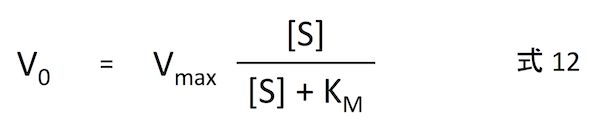
式 12 をプロットすると、下の図 (Public domain) のようになる。基質濃度が上がるほど反応速度は増えていくが、それは漸近的に V_max へ近づいてゆく。

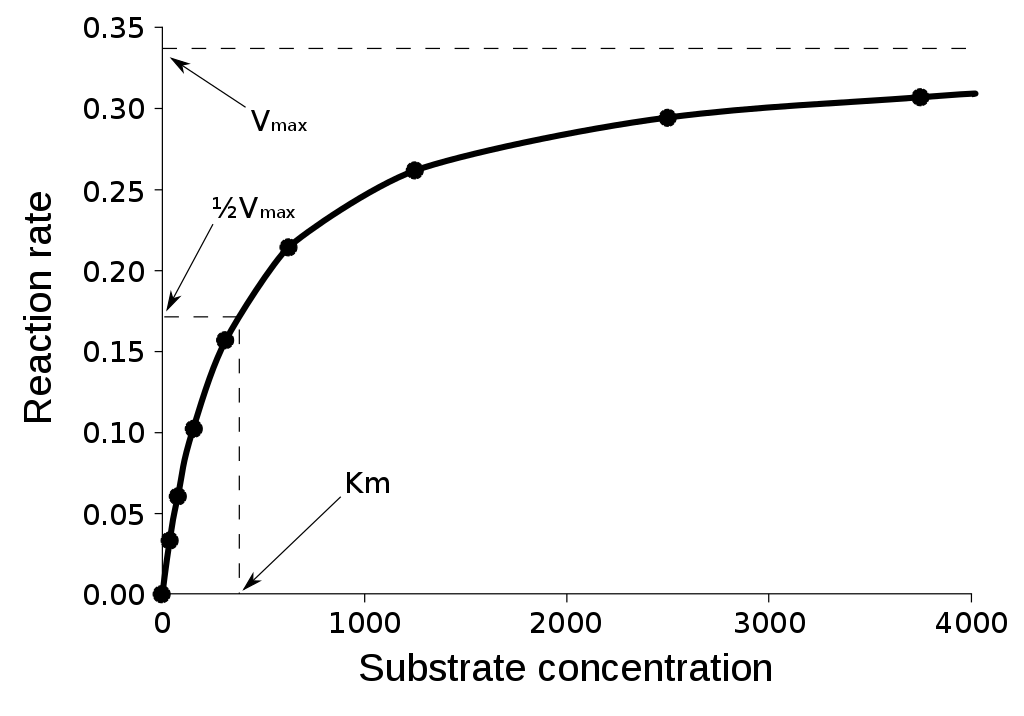
その他の画像 (7) も小さく載せておく。クリックで拡大可能。

説明的な事項

この式からわかるように、K_M は最終的に濃度の単位をもつ。これは式 7 の左辺からもわかる。ただし、式 7 の反応定数 k_-1, k₁, k₂ の単位は反応の種類によって異なるので、一連の結果は「k_-1, k₁, k₂ がそれぞれどんな単位であろうと、K_M としたときには濃度の単位になる」ことを示している。

また V_max は「この反応系における定数」という意味で「定数」のように扱っているが、実際は [E]_T に依存した変数であることも重要らしい (6)。なお、[E]_T は反応時間 0 ならば酵素と基質の結合も 0 であるから、[E]₀ と表されることもある。

K_M の解釈

基質が非常に豊富なとき、たとえば反応初期などの場合。

式 12 の分母 [S] + K_M ≈ [S] と考えてよく、[S] が約分されて V₀ = V_max となる。「基質が K_M << [S] を満たす程度多ければ、反応速度は最大になる」ということ。

反応速度式から [S] が消えてしまっていることに注意する。K_M << [S] の条件下では反応速度は一定で、基質の量に依存しない。これは 0 次反応 zero-order reaction である。

逆に基質が非常に少ない場合、[S] + K_M ≈ K_M となり、V₀ = (V_max / K_M) [S] である。 [S] ≈ 0 ということではないので、分子の [S] はそのまま残ることに注意。

このとき、反応速度は [S] の一次関数である。溶液中で酵素が余っていて、結合できる基質を探し求めている状態。基質が 2 倍になれば、そのまま反応速度も 2 倍になる。

式 12 に K_M = [S] を代入すれば、直ちにこの結論が導かれる。

よって「K_M の高い/低い酵素反応」という言い方が可能である。ある酵素反応の K_M が高いということは、基質濃度が相対的に高くならないと反応速度が上がらないということである。つまり、働き始めが遅いということ。Biochemistry ではアルコールデヒドロゲナーゼ の例が挙げられている。

関連項目

Michaelis-Menten の例外

アロステリック allosteric な制御を受ける酵素では、V と [S] のプロットがしばしばシグモイド型になり、Michaelis-Menten の規則に従わない (3)。

実験: Lineweaver-Burk plot

式 12 の両辺を逆数にすると、

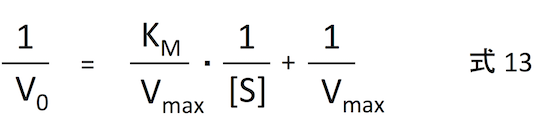
が導かれる。これは、1/V₀ と 1/[S] が直線関係になるということであり、漸近線が出てきてしまう 式12 よりもはるかに扱いやすい。これをプロットしたグラフを Lineweaver-Burk plot という。詳細は Lineweaver-Burk plot のページ で。

疑問点

もともと t = 0 に近いという条件で式変形を始めたので、上の図は常にその条件であり、V₀ と S₀ のプロットとして捉えるのが基本であろう。

試験管に酵素と基質を入れて反応が進んでいく状態を考えてみる。基質濃度がだんだん減っていく。このときの反応速度の変化は、基質濃度をちょっとずつ減らしながら何本も試験管を用意し、V₀ を測定したときの変化と同じようなものである。t = 1 の点を新たに t = 0 と定義しなおしていると言ってもよい。こう考えると、上のプロットは 1 本の試験管内で反応が進むときに V が徐々に減っていく状態を表したものとも言える・・・のか？

もちろん、「P の分解が起こらない」や、「反応に関与できる酵素の量が一定」などの仮定を保ったまま、理想的な条件下で考える必要があるが。

References

1. 小宮山、長棟 1997a (Book). 生命化学概論. 丸善株式会社.
2. ミカエリス・メンテンの式. Link.
3. Berg et al. Biochemistry, Seventh Edition: 使っているのは 6 版ですが 7 版を紹介しています。
4. 反応次数は反応式の係数からでも得られるのですか？ Link.
5. Schnell 2013a. Validity of the Michaelis-Menten equation - steady-state or reactant stationary assumption: that is the question. FEBS J 281, 464-472.
6. 知名、岡田 2014a (Review). 原典からの酵素反応速度論. 生物工学 92, 20-25.
7. GFDL, https://ja.wikipedia.org/w/index.php?curid=296690

コメント欄

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。