MRI の概要と目次

experiments/mri (NMR, MRI の目次)/mri
2018/05/23 更新


  1. 概要: MRI とは
  2. MRI 用語集
    • ボクセル
    • シグナル/ノイズ比
    • 空間分解能
    • 画像処理

広告

概要: MRI とは

核磁気共鳴画像法 MRI は、磁場内におかれたプロトン (水素原子核)の密度と、その状態を画像化する方法である。血流動態を可視化する機能的 MRI (functional MRI, fMRI) に対して、構造的 MRI (structural MRI, sMRI) と言うこともある。

右図 (6) のような画像が得られる。

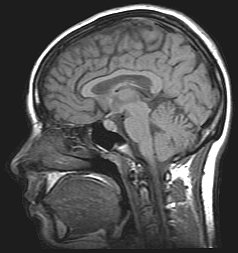
原理は核磁気共鳴 NMR であるが、共鳴周波数に重点を置く NMR と違って、水素原子の緩和状態に着目している。すなわち、特定のボクセル内にパルス状の電磁波でエネルギーを与え (共鳴)、電磁波の照射を停止してからの エネルギーの放出状態 (緩和状態)を主として画像化する (2)。

NMR に関する上記の説明 (共鳴周波数、核磁気共鳴など) がよくわからない場合には、まず NMR のメインページ を参照のこと。

続いて MRI を理解するためには、まず T1, T2 緩和から始めるのがよいと思う。私には この医師国家試験のための動画 がわかりやすかった。人によってしっくりくる説明が違うと思うので、多くの説明に触れるのがよい。基本概念が理解できれば、それぞれのサイトや教科書の説明が同じことを言っているのがわかってくるはずである。


T1 緩和、T2 緩和

以下、私が理解している内容を箇条書きでなるべくシンプルに述べてみる。

  1. プロトンはスピンしている (歳差運動)。
  2. 磁場の中に入れるとスピンの方向が揃う。しかし位相はばらばらである。
  3. RF パルスをかけると、プロトンが 90° 倒され位相が揃う。
  4. NMR では RF パルスの周波数と 化学シフト に注目しているが、MRI ではここからプロトンが起き上がってくる様子に注目する。
  5. T1 は縦方向 のベクトルである。よって RF パルス照射直後、プロトンが 90° 倒れているときに T1 はゼロで、起き上がるにつれて増大する。
  6. 一方、T2 は横方向 のベクトルである。よって RF パルス照射直後、プロトンが 90° 倒れているときに T2 は最大値をとり、プロトンが起き上がるにつれて減少する。
  7. T1 および T2 は、それぞれ T1 信号、T2 信号という電磁波として受信することができる。
  8. 組織によって T1 および T2 信号の変化のパターンが異なるので、これを利用して画像化する。

基本用語集

ボクセルと撮像範囲

MRI で撮像する範囲を FOV (field of view) という。単位は長さ (cm など)である。

MRI のデータは、ボクセル voxel (図のような立方体; 7)を単位として構成される画像である。一つの断面を写真のように示すのが一般的であり、この場合は単位はピクセル pixel になる。


たとえば、ピクセルの大きさが 1 mm 角、画像が 100 x 100 ピクセルのときには、FOV は 10 cm x 10 cm である。

ヒトの sMRI では、基準画像に合わせ込み registration を行った後のボクセル数は、サイズ 1.5 mm 角、121 (横) x 145 (縦) x 121 (スライス) = 2,122,945 voxels が一般的である (4)。

ヒトの fMRI ではボクセル数はこれより少なく、64 (横) x 64 (縦) x 49 (スライス) = 200,704 voxels 程度である。ただし、fMRI の場合は経時的な測定を行うため、さらに100点程度の時間の次元が加わる (4)。


シグナル/ノイズ比

シグナル/ノイズ比 (SNR, signal to noise ratio)は他の実験でも重要な概念であり、MRI の場合には

SNR = 信号強度の平均値/ノイズの標準偏差

SNR = k * (voxel volume) * (number of repetition)1/2 / (bandwidth)1/2

などの式で表される値である (3)。なお、k は定数、number of repetition は計測回数、bandwidth は帯域幅 (周波数の範囲、単位はHz)である。結局のところ、実際に測定してみないと分からないことが多い。


空間分解能 Spatial resolution

隣接する2つの点を個別かつ明瞭に識別する能力。実際には、識別できる距離のうち最も短いものを 空間分解能 spatial resolution ということが多い。ただしこの定義は機器によって様々であり、例えば望遠鏡では角度で規定されている。

「もっとも短い」ことを含めていない説明が多いが、これを考えないと機器の性能としての空間分解能の意味がなくなるため必要であると思われる。一般的な画像診断機器においては、CT > MRI > PET である。

空間分解能を高くすると、SNR は低下する (3)。


> ラット 脳の ex vivo 構造的 MRI で、0.16 x 0.16 x 0.16 mm 3 の解像度が得られている (5)。
  • 9.4 T, 3D multiple-spin echo DW sequence. TR = 700 ms, TE = 30 ms.

画像処理

得られた画像はそのまま解析に使われるわけではなく、一般に以下のような前処理が必要である (4)。

リアラインメント Realignment

主に頭位置補正 (head motion correction)とスライス補正 (slice-timing correction)がある (4)。いずれも fMRI で使われる。

対象が fMRI scan 中に動いた場合、その位置を補正して解析を行う必要がある。これが head motion correction である。平行移動 (x, y, z) 　と回転 (pitch, roll, yaw) の6つのパラメーターから成る剛体変換 rigid body transformation が使われる (4)。

また、fMRI では1スライスの撮影に数秒を要するため、スライス間で時間のずれが生じる。これを補正するのが slice-timing correction である (4)。

セグメンテーション Segmentation

画像データを灰白質 gray matter, 白質 white matter, 脳脊髄液 cerebral spinal fluid に分割することをセグメンテーション segmentation という (4)。さらに細かく、解剖学的な区分を与えることも segmentation と呼ばれる。

解剖学的標準化 Registration

脳の形は対象者 (個体)ごとに異なるので、比較するためには標準画像への位置合わせを行う必要がある (4)。これを spatial normalization という。Spatial normalization という表現もある。

平滑化 Smoothing

ボクセル値の過度な変動を抑えるため、値の平滑化 smoothing が最終的に行われる (4)。ガウス型関数による畳み込みなどが使われる。
広告

コメント欄

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。

References

1. 今西ほか 2009a (Book). 心から納得・理解できるMRI原理とMRS. 医療科学社.

イラストを多用した、わかりやすい MRI と MRS の本。基本的に見開きの左が文章、右がイラストという構成。

MRS および MRS で検出できる代謝産物について詳しく解説している本は、日本語では少なく貴重である。NAA や クレアチンといった代謝産物の機能と測定法の概要が書かれている。

もう一つの特徴は、MRI 原理の説明に回転座標系が使われていないこと。そのため、他の教科書とはちょっと異なる説明の仕方になっている。MRI の原理を理解するのは難しいので、色々な方向から眺めてみるという点でもお勧めの一冊である。私が T1, T2 relaxation を理解できたのはこの本のおかげ。
  1. 15分で分かる (？)MRI part 1: http://www5.dent.niigata-u.ac.jp/%7Enisiyama/MRI-15-min.pdf
  2. MRI画像の画質とMR信号のアーチファクト: http://www.clg.niigata-u.ac.jp/~tsai/home-page/lecture/MRI-artifacts-quality.pdf
  3. 川口 2012a. 脳MRIデータの統計解析. 計量生物学 33, 145-174.
  4. Zhang et al. 2007a. Unique pattens of diffusion derectionality in rat brain tumors revealed by high-resolution diffusion tensor MRI. Magn Reson Med 58, 454-462.
  5. "MRI brain". Licensed under パブリック・ドメイン via ウィキメディア・コモンズ.
  6. "Voxels" by No machine-readable author provided. Vossman assumed (based on copyright claims). - No machine-readable source provided. Own work assumed (based on copyright claims).. Licensed under CC 表示-継承 2.5 via ウィキメディア・コモンズ.

↑