集団遺伝学: ハーディー・ワインベルグの法則

other_topics/genetics/population_hardy-weinberg
2017/11/28 更新

ハーディー・ワインベルグの法則 (2 アリル)

2 アリルの場合のハーディー・ワインベルグの法則は以下のように表される (3)。頻度、遺伝子型などの集団遺伝学用語の意味については、集団遺伝学の用語集のページを参照のこと。

以下の仮定 (2) のもとで、四角で囲んだ関係が成立するというのがハーディー・ワインベルグの法則である。

2 個のアリル A, a の集団内の頻度がそれぞれ p および q の場合 (p + q = 1)、3 つの遺伝子型 (AA, Aa, aa) の頻度はそれぞれ p², 2pq, q² となる。また p² + 2pq + q² = 1 である。

遺伝子型の頻度は、しばしば f(AA), f(Aa), f(aa) のように表される。この表記を用いると

が成立するのがハーディー・ワインベルグの法則であると言える。この法則を説明するための図を、解説とともに 2 つ載せておく。

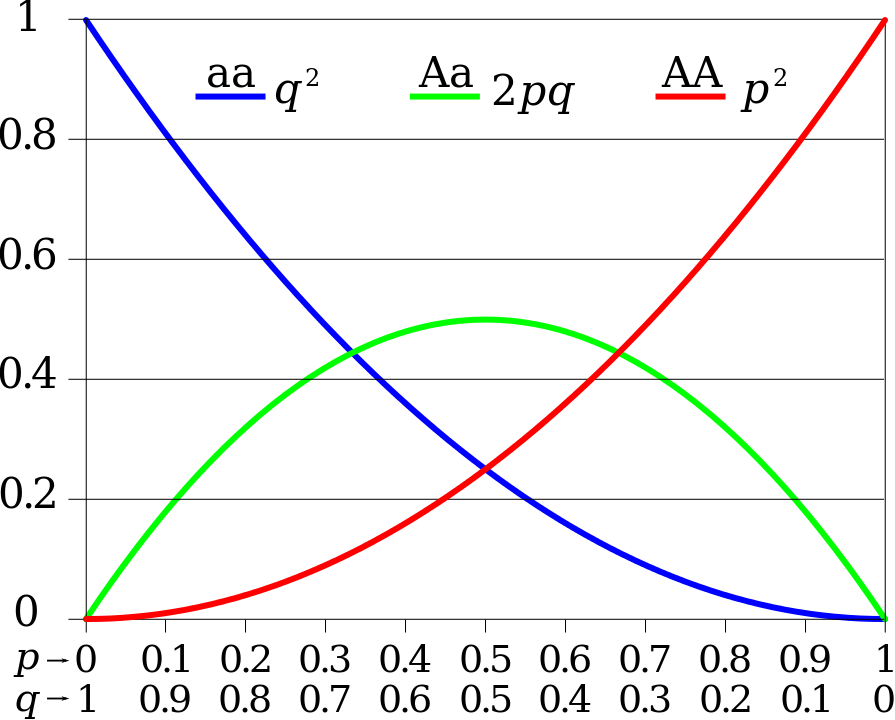
最初の図 (Ref 4) は、単に法則を図にしたものである。縦軸が遺伝子型の頻度を示し、横軸はアリル頻度である。p + q = 1 が成り立っており、横軸には p および q の値が両方書かれている。

まず、極端な場合を見てみよう。図の左端のようにアリル頻度が p = 0 かつ q = 1 の場合、全ての個体が aa になり、遺伝子型の頻度 f(aa) = 1 となる。同様に、図の右端のように p = 1 のとき f(AA) = 1 となる。

f(Aa) は p = q = 0.5 のときに最大となり、その値は 2pq = 0.5 である。

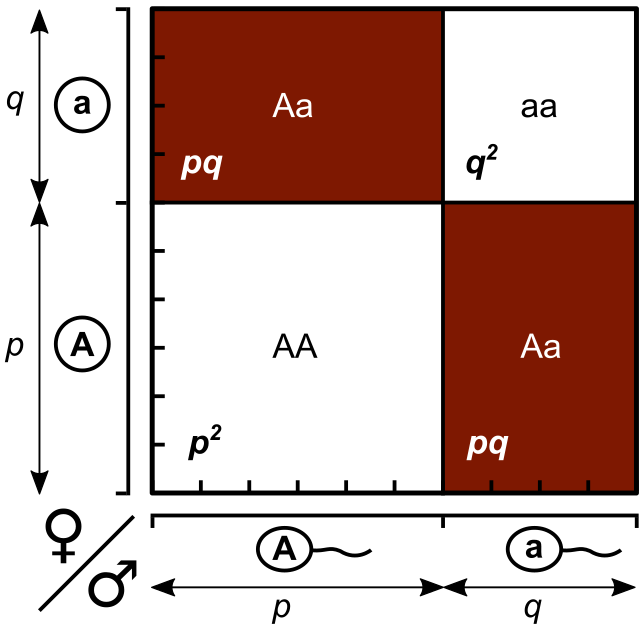
2 番目の図 (Ref 5) は、メンデル遺伝で使われる Punnett square を使ってこの法則を説明したものである。遺伝子型の頻度が面積で表されるのがおもしろい。

この法則の重要性は一見わかりにくい。これだけは知っておきたい図解ジェネティクス (Amazon link) には、集団における「遺伝子型」の頻度と「アリル頻度」の間の関係を明示したことがこの法則の重要な点であると書かれている (3)。

この法則はシンプルだが奥が深く、式を適用することでさまざまな現象を予言することができる。以下、具体例を挙げつつ本法則の適用例を紹介する。

ハーディー・ワインベルグの法則の重要な解釈の一つが、上記の条件が満たされる限りアリル頻度は世代が経過しても変化しないということである。

これは実例で考えた方が良いだろう。

アリル a を劣性遺伝病の遺伝子とすると、AA および Aa の遺伝子型をもつ人は健康、aa の人が病気という表現系 phenotype を示す。この病気は集団内で 1 万人に 1 人という珍しい遺伝病であるとする。

このとき、集団内の患者の頻度から q² = 1/10,000 すなわち q = 1/100 = 0.01 である。p + q = 1 より、p = 0.99 となる。

遺伝病の遺伝子のキャリア Aa の集団内における割合は 2pq で与えられる。つまり 2 x 0.99 x 0.01 = 0.0198 であり、集団の約 2% がキャリアということになる。これは 1 万人に 1 人という頻度から直感するよりも多いのではないだろうか？

集団が上記の条件を満たす限りアリル頻度は変化しないので、世代が変化しても常に 2% は遺伝病のキャリアであり続けるということになる。

3 アリルの場合も、基本的な考え方は同じである。上記の仮定のもとで、

3 個のアリル A₁, A₂, A₃ の集団内の頻度がそれぞれ p₁, p₂, p₃ の場合、(p₁ + p₂ + p₃ = 1)、任意交配のもとでは遺伝子型の頻度は以下のようになる (2,3)。

また、これらの頻度を全て足すと 1 になる。

ABO 血液型がこの実例にあたる (3)。3 アリルだと計算が複雑になるのでここには書かないが、遺伝病の場合と似たような結論が得られる。

つまり O 型のアリルは劣勢なので、実際に O 型の人がいる頻度以上に O 型のアリルの頻度が高いということである。劣勢の遺伝病に意外と多くのキャリアがいることと同じように考えて良いだろう。

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。