気体定数: ボイル・シャルルから導かれる定数

UBC/math_physics/constant/gas_constant

このページの最終更新日: 2024/12/15

ボイルの法則: Boyle's law

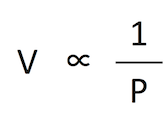
1661 年、ボイル Boyle は「一定量の気体の体積は、温度が一定ならば圧力に逆比例する」ことを発見した (1)。これが Boyle's law である。

この式は、温度一定の条件下で PV = k (k は定数) とも表せる。これがボイルの法則 Boyle's law である。感覚的に非常に理解しやすいので、小さい頃は「ボイルはコレ適当に言ってみただけじゃないだろうか？」と思っていた。今でも少し思っている。

ボイル・シャルルと一緒にされることが多いが、シャルル Charles の研究は Boyle から 100 年以上もあとのことである。Gay-Lussac の研究と合わせて「圧力が一定のとき、体積は温度に比例して増加する」ことがわかった。つまり

V ∝ T (P = 一定のとき)

比例関係なので、V/T が常に一定の値をとるということになる。

この 2 つの式から状態方程式を導出する。式変形はシンプルである。

ステップ 1.

圧力、体積、温度がそれぞれ P₁, V₁, T₁ である気体 (P₁, V₁, T₁) を考える。この気体を温度一定のまま体積 V₁' まで変化させたときの圧力を P₂ とする。つまり(P₂, V₁', T₁) という状態を想定する。

このとき、ボイルの法則から

P₁V₁ = P₂V₁' (式 1)

である。

ステップ 2.

(P₂, V₁', T₁) を、さらに状態 (P₂, V₂, T₂) まで変化させる。この変化は圧力が一定で温度を変化させるものなので、シャルルの法則を適用して

V₁'/T₁ = V₂/T₂ (式 2)

である。両辺に T₁ をかけると

V₁' = V₂T₁/T₂ (式 3)

ステップ 3.

式 3 を式 1 に代入すると、

P₁V₁ = P₂V₂T₁/T₂ (式 4)

これを整理すると

P₁V₁/T₁ = P₂V₂/T₂ (式 5)

となり、任意の 2 つの状態で PV/T が一定の値をとることが示された。気体を 1 mol と仮定した場合のこの値を気体定数 gas constant といい、R で表す。気体が n mol あるとき、P および T は量の影響を受けないが、V は nV となる。よって状態方程式は

PV = nRT (式 6)

となる。気体定数は実験的に求められ、現在では R = 8.3145 J K^-1mol^-1 が用いられている。

式 6 から単位は (圧力 x 体積)/(温度 x mol) である。各単位の次元を簡単に復習しておく。

R の次元は ML²T^-3mol^-1 になるが、エネルギーの次元 (力 x 距離、箱を押す状況を考えよう。ML²T^-2) を分子にもってくるとエネルギー/温度 • mol になり、上の単位になる。

熱平衡状態にある理想気体は、P, V, T, n の熱力学変数で記述することができる (1)。状態方程式 PV = nRT は、このうち 3 つを決めると残りの 1 つが自動的に決まってしまうことを示している。

系の体積 V およびモル数 n (質量 m も n の関数である) を示量変数といい、その値が系に含まれる物質の全量に依存する。一方、圧力 P および温度 T は示強変数であり、系のそれぞれの点で確定した値をもつ。

サーバー移転のため、コメント欄は一時閉鎖中です。サイドバーから「管理人への質問」へどうぞ。